Khối cầu là gì?
Khối cầu là một hình dạng 3D hoàn hảo, giống như một quả bóng. Mọi điểm trên bề mặt của nó đều cách đều một điểm ở trung tâm, gọi là tâm. Khoảng cách từ tâm đến bề mặt gọi là bán kính. Khối cầu xuất hiện phổ biến trong tự nhiên và cuộc sống hàng ngày. Ví dụ như: trái đất (gần như hình cầu), bóng đá, bóng bàn, bi-a, giọt nước, bong bóng xà phòng…Hiểu về khối cầu giúp chúng ta giải thích nhiều hiện tượng tự nhiên và thiết kế các sản phẩm công nghiệp hiệu quả.

Thể tích khối cầu
Vậy thể tích khối cầu là gì? Nói đơn giản, đó chính là lượng “chất’ bên trong quả cầu. Hãy tưởng tượng bạn có một quả cầu thuỷ tinh rỗng. Thể tích của nó chính là lượng nước mà bạn có thể đổ vào bên trong quả bóng đó cho đến khi nó đầy. Đối với các vật thể đặc như quả cam hay quả bóng bi-a, thể tích là toàn bộ phần bên trong của chúng.
Thể tích khối cầu được đo bằng đơn vị khối như mét khối (m³), centimét khối (cm³), hoặc lít. Nó phụ thuộc vào kích thước của khối cầu, cụ thể là bán kính của nó.

Công thức tính thể tích khối cầu
Thể tích của khối cầu được tính bằng công thức:
V = (4/3) × π × r³
Trong đó:
V là thể tích của khối cầu
π (pi) là hằng số toán học, xấp xỉ 3,14159
r là bán kính của khối cầu
Công thức này được phát triển bởi nhà toán học Archimedes và là một thành tựu toán học quan trọng trong lịch sử.
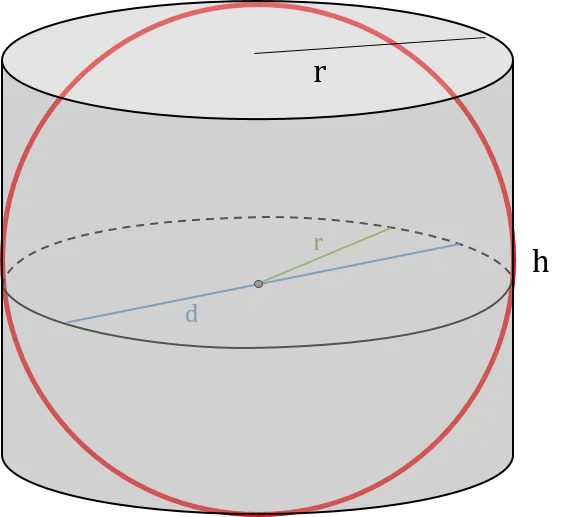
Để hiểu rõ hơn về công thức này, ta có thể so sánh với thể tích của một hình trụ:
Thể tích hình trụ: V = π × r² × h (với h là chiều cao)
Thể tích khối cầu: V = (4/3) × π × r³ = (4/3) × π × r² × r
Ta thấy thể tích khối cầu bằng 4/3 lần thể tích của một hình trụ có bán kính đáy bằng bán kính khối cầu và chiều cao bằng bán kính.
Các bước giải bài tập tính thể tích khối cầu đơn giản nhất
Để giải các bài tập về thể tích khối cầu, ta thường theo các bước sau:
Bước 1: Xác định dữ kiện
Đọc kỹ đề bài để tìm ra thông tin về bán kính hoặc đường kính của khối cầu.
Nếu đề bài cho đường kính, chia đôi để có bán kính.
Bước 2: Áp dụng công thức
Sử dụng công thức V = (4/3) × π × r³
Thay giá trị bán kính vào công thức
Bước 3: Tính toán
Thực hiện phép tính, chú ý quy tắc ưu tiên trong toán học
Làm tròn kết quả theo yêu cầu của đề bài (nếu có)
Bước 4: Kiểm tra và trình bày kết quả
Kiểm tra lại các bước tính toán
Ghi rõ đơn vị đo thể tích (thường là m³, cm³, hoặc mm³)
Ví dụ : Hãy tính thể tích của một quả bóng có bán kính 10 cm.
Giải:
Bước 1: Bán kính r = 3 cm
Bước 2: Áp dụng công thức V = (4/3) × π × r³
Bước 3: V = (4/3) × 3,14 × 3³ = (4/3) × 3,14 × 27 ≈ 113,03 cm³
Bước 4: Thể tích của quả bóng là khoảng 113,03 cm³
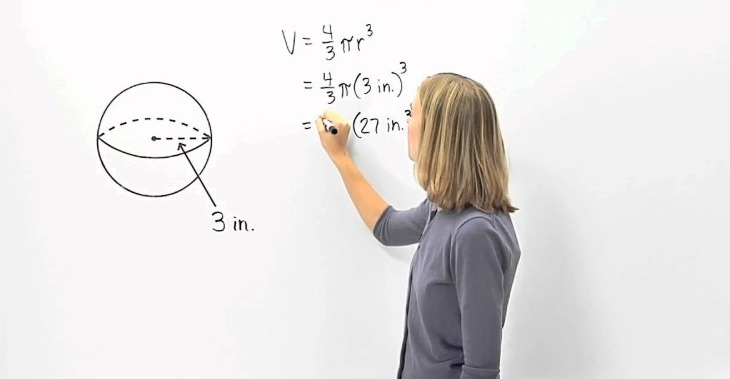
Bài tập vận dụng tính thể tích của khối cầu có lời giải
Để giúp các bạn học sinh và phụ huynh hiểu rõ hơn cách áp dụng công thức tính thể tích khối cầu, chúng ta hãy cùng giải quyết một số bài tập thực tế. Những ví dụ này sẽ không chỉ rèn luyện kỹ năng tính toán mà còn cho thấy sự liên quan của kiến thức này trong cuộc sống hàng ngày.
Bài tập 1: Một quả địa cầu có đường kính 30 cm. Tính thể tích của quả địa cầu này.
Lời giải:
Bước 1: Xác định dữ kiện
Đường kính = 30 cm
Bán kính r = 30/2 = 15 cm
Bước 2: Áp dụng công thức
V = (4/3) × π × r³
Bước 3: Tính toán
V = (4/3) × 3,14 × 15³
= (4/3) × 3,14 × 3375
≈ 14137,17 cm³
Bước 4: Kết luận
Thể tích của quả địa cầu là khoảng 14137,17 cm³ hay 14,14 lít.
Bài tập 2: Một khối cầu có thể tích 4188,8 cm³. Tính bán kính của khối cầu đó.
Lời giải:
Bước 1: Xác định dữ kiện
Thể tích V = 4188,8 cm³
Bước 2: Áp dụng công thức và biến đổi
V = (4/3) × π × r³
4188,8 = (4/3) × 3,14 × r³
r³ = 4188,8 × 3 / (4 × 3,14)
r³ ≈ 1000
Bước 3: Tính toán
r = ³√1000 = 10 cm
Bước 4: Kết luận
Bán kính của khối cầu là 10 cm.
Bài tập 3: Một bể chứa nước hình cầu có đường kính trong 6 m. Tính thể tích nước tối đa mà bể có thể chứa.
Lời giải:
Bước 1: Xác định dữ kiện
Đường kính = 6 m
Bán kính r = 6/2 = 3 m
Bước 2: Áp dụng công thức
V = (4/3) × π × r³
Bước 3: Tính toán
V = (4/3) × 3,14 × 3³
= (4/3) × 3,14 × 27
≈ 113,04 m³
Bước 4: Kết luận
Thể tích nước tối đa mà bể có thể chứa là khoảng 113,04 m³ hay 113.040 lít.
Bài tập 4: Một quả bóng bay hình cầu được bơm từ bán kính 10 cm lên đến bán kính 15 cm. Tính tỉ lệ tăng thể tích của quả bóng.
Lời giải:
Bước 1: Xác định dữ kiện
Bán kính ban đầu r₁ = 10 cm
Bán kính sau khi bơm r₂ = 15 cm
Bước 2: Tính thể tích ban đầu và sau khi bơm
V₁ = (4/3) × π × r₁³ = (4/3) × 3,14 × 10³ ≈ 4186,67 cm³
V₂ = (4/3) × π × r₂³ = (4/3) × 3,14 × 15³ ≈ 14137,17 cm³
Bước 3: Tính tỉ lệ tăng
Tỉ lệ tăng = (V₂ - V₁) / V₁ × 100%
= (14137,17 - 4186,67) / 4186,67 × 100%
≈ 237,67%
Bước 4: Kết luận
Thể tích của quả bóng tăng khoảng 237,67%.
Một số công cụ hỗ trợ tính thể tích khối cầu
Trong thời đại công nghệ số, việc tính toán thể tích khối cầu trở nên dễ dàng hơn bao giờ hết nhờ các công cụ trực tuyến và ứng dụng di động. Dưới đây là một số công cụ hữu ích giúp bạn tính toán nhanh chóng và chính xác:
WolframAlpha: Không chỉ tính toán mà còn cung cấp thông tin chi tiết về các khái niệm toán học liên quan.
GeoGebra 3D Calculator: Cho phép bạn mô phỏng và tính toán các hình khối 3D, bao gồm khối cầu.
Geometry Calculator: Tập trung vào các phép tính hình học, bao gồm thể tích khối cầu.
OmniCalculator - Sphere Calculator:Tính nhanh thể tích, diện tích bề mặt và các thông số khác của khối cầu.
Việc sử dụng các công cụ này không chỉ giúp bạn tiết kiệm thời gian mà còn tăng độ chính xác trong tính toán, đặc biệt khi làm việc với các số phức tạp. Tuy nhiên, hiện tại các công cụ chỉ hỗ trợ bản Tiếng Anh nên sẽ có một số hạn chế với người dùng. Để hiểu sâu về khái niệm thể tích khối cầu, bạn vẫn nên thực hành tính toán thủ công trước khi sử dụng các công cụ hỗ trợ.
Bằng cách kết hợp kiến thức lý thuyết với các công cụ tính toán hiện đại, bạn sẽ nắm vững kỹ năng tính thể tích khối cầu và áp dụng hiệu quả trong học tập cũng như trong các ứng dụng thực tế.
Ứng dụng thực tế của thể tích khối cầu
Kiến thức về thể tích khối cầu không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng quan trọng trong đời sống và khoa học. Ở một số lĩnh vực sự hiểu biết về thể tích khối cầu đóng vai trò then chốt như:
Trong lĩnh vực thiên văn học, kiến thức này để tính toán kích thước của các hành tinh và vệ tinh, đồng thời ước tính khối lượng của các thiên thể dựa trên thể tích và mật độ.
Trong lĩnh vực kỹ thuật và công nghiệp sử dụng để thiết kế bồn chứa hình cầu, cũng như tính toán lượng vật liệu cần thiết để chế tạo các vật thể hình cầu.
Trong thể thao, kiến thức về thể tích khối cầu giúp kiểm tra tiêu chuẩn và áp suất của bóng dựa trên thể tích.
Trong y học, giúp bác sĩ ước tính thể tích các cơ quan hình cầu như mắt hoặc u bướu, cũng như tính liều lượng thuốc dựa trên thể tích cơ thể.
Ngoài ra, các sáng tạo trong kiến trúc và nghệ thuật cũng được lấy cảm hứng từ thể tích khối cầu. Nổi bật có thể kể đến như Apple Store Vịnh Marina Singapore của Foster + Partners với thiết kế như treo lơ lửng trên mặt nước. Thư viện công cộng Thiên Tân ở Trung Quốc gây ấn tượng với thiết kế như con mắt khổng lồ.
Tóm lại, hiểu biết về thể tích khối cầu không chỉ giúp chúng ta giải quyết các bài toán trong lớp học, mà còn mở ra cánh cửa cho vô số ứng dụng thực tế trong cuộc sống.
Tổng kết
Thể tích khối cầu là một khái niệm cơ bản nhưng quan trọng trong toán học và khoa học. Công thức V = (4/3) × π × r³ cho phép chúng ta tính toán chính xác thể tích của bất kỳ khối cầu nào khi biết bán kính. Hiểu và áp dụng được công thức này không chỉ giúp giải quyết các bài toán học thuật mà còn có nhiều ứng dụng thực tế trong đời sống và công nghiệp. Qua các bài tập và ví dụ, chúng ta thấy rằng việc tính toán thể tích khối cầu không quá phức tạp nếu nắm vững công thức và các bước giải. Tuy nhiên, điều quan trọng là phải hiểu rõ bản chất của khối cầu và ý nghĩa của các thành phần trong công thức. Hi vọng qua những chia sẻ về thể tích khối cầu trong bài viết này. Pico đã giúp bạn hiểu rõ hơn và có thể vận dụng các kiến thức một cách nhanh chóng và linh hoạt nhất.













